资料汇总
李宏毅2019课程
- 机器的错觉(Adversarial Attrack)
- 如何避免?
- 测试资料和训练资料分布不一样的时候该如何处理?

- Unsupervised Domain Adaptation

- 异常检测Anomaly Detection
- 检测输入数据跟训练数据集是否相似

- 应用:诈骗检测、网络入侵检测、癌症检测等
- https://www.kaggle.com/ntnu-testimon/paysim1/home
- http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html
- https://www.kaggle.com/uciml/breast-cancer-wisconsin-data/home
- 检测任务是否属于辛普森家族成员:https://www.kaggle.com/alexattia/the-simpsons-characters-dataset/
- 如何预估置信区?

- 你会发现检测数值分布比较均匀,如果都达不到阈值,那么则很大程度表示该任务不属于;如果分布不均匀,最大的值大于阈值,那么就属于该预测值【这里面涉及期望、方差、熵】
- 论文:TerranceDeVries, Graham W. Taylor, Learning Confidence for Out-of-Distribution Detection in Neural Networks, arXiv, 2018
- Training Set、Dev Set、Testing Set
- 评估系统好坏的指标:
- 正确率:单纯按照正确率来衡量会受到正常数据跟异常数据量比例的影响,如果异常数据占比很小,那么如果按照某个阈值来判定,得到的正确率都会很高,而这并不能真正的反映模型的好坏
- 模型预测会存在两种情况:一是正确的误判为错误的;二是错误的错判为正确的。这两种情况根据不同的业务场景,其权重是不一样的;举例来说,如果系统更看重正确的误判为错误的情形,那么在衡量系统好坏的时候,每笔误判权重要大于错误的判定为正确的情形;反之亦然;比较现实的例子就是癌症检测,如果有一次检测误判为癌症,那么患者可以选择去其他医院复查一下即可,但是如果本来患了癌症系统却检测没病,这样就会耽误治疗,影响就大了。
- 二分类的问题中,主要的评价指标有precision、recall、F-score以及ROC曲线等。我们主要关心的是测试集的正样本能否正确分类,当样本不均衡时,比如样本中负样本数量远多于正样本,此时如果负样本能够全部正确分类,而正样本只能部分正确分类,那么(TP+TN)可以得到较高的值,也即Accuracy是个较大的值。这种情形下正样本并没有取得良好的分类效果。【precision=TP/(TP+FP)、recall=TP/(TP+FN)】
- 模型训练过程训练数据集的feature的权重不一,如果某一个feature权重占比较高,那么在检测的时候就很有可能输入的数据在该特征上比较相符而导致置信分数过高,就不可避免会产生误判,这种情况该如何解决?
林轩田的课程
- 机器学习的个人理解
- 以电商为例,简单来说就是用户浏览页面商品的点击数据(历史浏览数据),结合某些特征维度进行训练,这个训练的过程是由具体的算法来执行,最终会生成一个预测模型,这个预测模型就是从这些历史数据中挖掘出来一些规律,之后对于新的用户以及新的商品,就能够根据某些特征来进行用户喜好,可能性购买的一种预测,进而作出个性化的推荐。
- 这里机器学习的模型到底是个什么东西?人们往往在学习某个东西之后会产生自己的技能,但是这个技能是个抽象的东西,对应到机器学习的模型,就很难想象它到底可以具象成一个什么东西;实际上,简单理解,这个学习得到的模型就是映射。从数学的角度来理解就是函数,给定输入集合的一个元素,函数会唯一的对应一个输出值。
- 比如函数:$w_1x_1 + w_2x_2+…+w_dx_d+b$,当$w_1,w_2,…,w_d$是确定的,那么给定一组$x_1,x_2,…,x_d$就能够唯一确定输出值$f(x)$。手淘的有好货其实就是这样的例子。
- 机器学习解决的是哪类问题呢?
- 难以用规则解决的问题可以尝试用机器学习来解决
- 算法导论中经典的排序问题,无论是快排还是归并排序,解法都是一些确定的规则;而对于机器学习问题,比如垃圾邮件识别、识别一张图片上的物体是不是树叶等,这些就很难用一个确定的规则来解决,前者是由于很难穷举,而后者则是由于很难去描述树叶的规则。
- 由前面的历史浏览数据来训练模型的实例可以看出历史数据中隐藏着用户是否会点击某个商品的某种规律。所以机器学习应用的一个必要条件就是:有大量数据,并且数据中有隐藏的某种规律或模式
- 由此得知机器学习的三要素就是:数据+学习算法+模型(映射)
- 接下来将借助于PLA算法的实例来具体说明机器学习的应用:
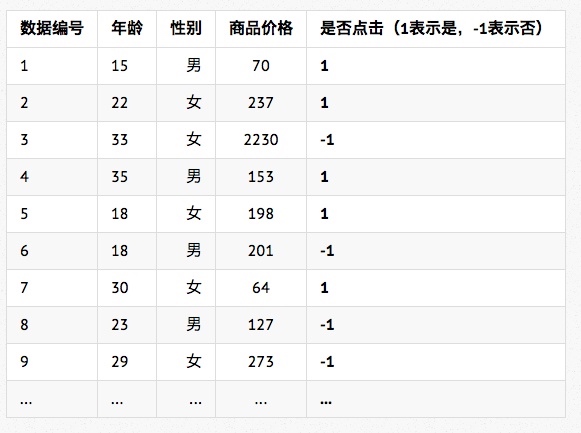
- 上图展示的是一份样本数据,该训练数据的每一行称为一个训练样本;注意到每个样本包含三个属性:年龄、性别和商品价格。代表了我们认为用户是否会点击该商品取决于这三个因素,但实际上影响用户点击的因素远不止这三个因素,这里是简化处理。这些属性我们统一称之为特征(feature)。在该场景中,我们还需要对用户是否点击商品进行预判,这个预判结果也需要记入这个模型系统之中,因此是否点击这个信息被记做标注(label)。
- 上述这份训练数据是从哪里来的?绝大多数互联网产品都会把用户的行为数据——包括浏览历史、点击历史记录下来,我们称为日志(Log)。从日志数据中就能知道每个用户点过什么商品(对应标注为1的样本),看了什么商品却没有点(对应标注为-1的样本),再关联上用户的特征数据(年龄、性别)和商品的特征数据(价格),就得到学习算法所需要的训练数据了。
解释一下上面提到的数据是否有标注:根据标注有无可以将机器学习分成有监督和无监督两类。
- 监督学习:每个输入样本都有标注,这些标注就像老师的标准答案一样”监督“着学习的过程。而监督学习又大致分成两类:分类(Classification)和回归(Regression):
- 分类问题:标注是离散值,比如用户”点击“和”不点击“。如果标注只有两个值,则称为二分类,如果标注有多个值,则称为多分类。
- 回归问题:标注是连续值,比如如果问题是预测北京市房屋的价格,价格作为标注就是一个连续值,属于回归问题。
-
无监督学习:训练样本没有标注,无监督学习解决的典型问题是聚类(clustering)问题。比如对一个网站的用户进行聚类,看看这个网站用户的大致构成,分析下每类用户群的特点是什么。
- 继续回到上面的实例,其中的映射关系说明如下:
- 映射的输入:
- 输入样本用符号$x$表示,第$i$个样本记作$x_i$
- 每个样本有三个特征,于是样本$x_i$又可以被写成向量$x_i = (x_{i1},x_{i2},x_{i3})$,其中$x_{i1}$表示年龄,$x_{i2}$表示性别,$x_{i3}$表示商品价格,也称之为特征向量
- 所有特征向量的集合就是总的输入集合,该例子中本质上是三个三维向量张成的三维空间,称之为样本空间,记作$X$;任意输入的$x$都是这个3维样本空间的一个向量,用符号表示就是$x\in X$
- 映射的输出
- 输出的样本标注用$y$表示,第$i$个样本的标注记作$y_i$
- 该例中只存在-1和1两种取值的标注,采用一个一维向量即可表示$y=y_{i1}$。该一维向量张成的空间即为标注空间,记作$Y$,用符号表示就是$y \in Y$。
- 映射的表示
- 如此机器学习模型就是输入空间$X$到输出空间$Y$的一个映射,将映射用$g$表示就是:$g: X \to Y$。
- 映射的输入:
- 接下来问题的关键是如何找到这个映射函数呢?到底存不存在一个完美的映射函数可以百分百预测所有的输入呢?
- 不妨假设存在这样一个完美的映射$f$,它不仅能够对训练数据中的所有样本都能够正确的预测用户是否点击,对于遇到的新的样本也是一样的。但是现实中并不存在这样的完美模型(Ground Truth),也称之为目标模型,也即这个完美模型(函数)是未知的。既然不存在,那我们如何以它为目标来学习呢?这时我们就只能依赖训练数据,当训练数据足够多的时候,我们就可以认为海量的样本反映了Ground Truth f的样子,我们就称这种情况为训练数据来自于f。
- 假设了Ground Truth f的存在,那么学习算法要做的就是找出某个映射,使得这个映射尽可能的接近f。在实际训练过程中,学习算法会有一个假设集合(Hypothesis Set,记作H),这个集合包含所有候选的映射函数。学习算法做的事情就是从中选出最好的g,使得g越接近f越好。
- 接下来采用一个示例来说明假设函数的情况:
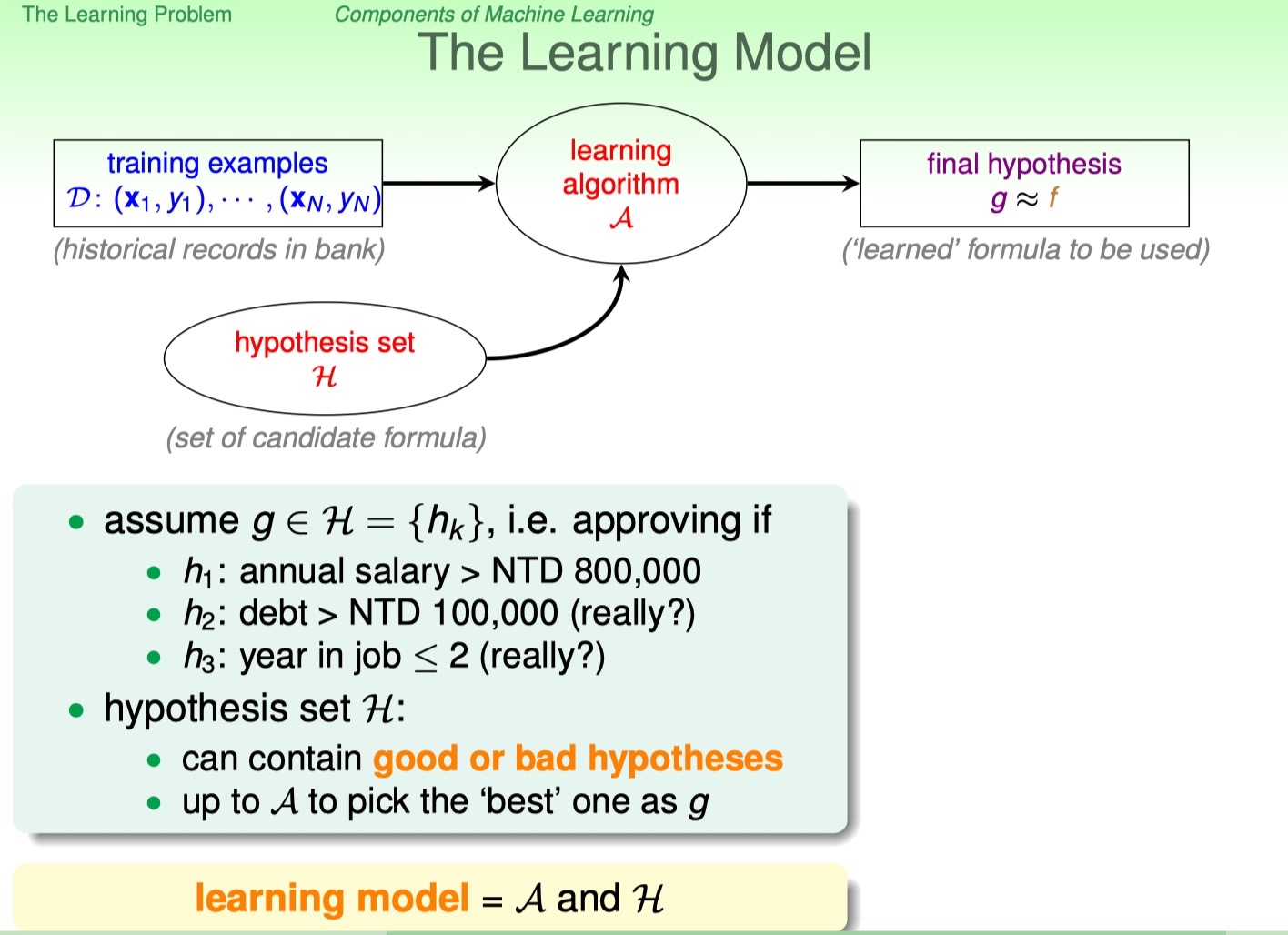
- 银行核定是否要发放信用卡给客户,那可能的假设函数(判定函数)就是上图中的三个:1、年收入是否超过80万台币; 2、负债超过10万台币; 3、工作不满两年;我们要做的就是从这三个假设函数中筛选一个最好的最为$g$。
- 接下来继续最开始的实例,我们将引入一个PLA的算法,全称 Perceptron Learning Algorithm。其中 Perceptron 译作感知机,它是人工神经网络中最基础的两层神经网络模型。
- 经典的PLA算法问题存在着两点性质:1、算法可能永远也无法运行结束,会迷失在茫茫的训练数据中永远找不到出口;2、哪怕知道PLA最终能找到出口,我们也无法事先知道学习需要花多久;但是对于上述两个问题可以通过算法的升级版加以解决
-
PLA的基本思路: * 每个特征都有一个权重$W_i$表示该特征的重要程度,综合所有的特征和权重计算一个最终的分数,如果分数超过某个阈值(threshold),就表示用户会点击,否则不会点击。
- 我们进一步简化训练数据,将特征缩减为两个:年龄和商品价格
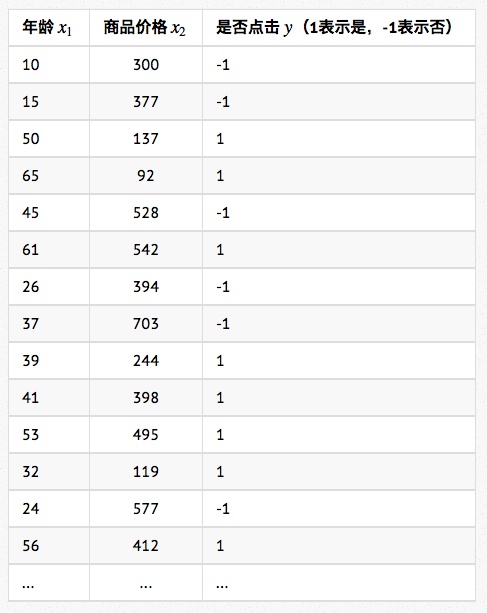
- 如上图所示,每一条样本表示为$x=(x_1, x_2)$,其中$x_1$表示年龄,$x_2$表示商品价格。样本标注用$y$表示,$y=1$表示用户点击,$y=-1$表示用户没有点击。我们将特征的权重记作$w = (w_1, w_2)$,$w_1$代表了年龄这维特征的重要性,$w_2$代表商品价格这维特征的重要性。于是判断一个用户会不会点击,就变成了下面这个函数:
- 将该函数进行简单的变换,可以采用符号函数$sign(x)$来表示:当$x>0$, $sign(x)=1$;当$x<0$, $sign(x)=-1$。
- 不同的$w_i$和$threshold$对应了不同的函数,所有可能的值的集合构成了构成了PLA的假设集合(Hypothesis Set),叫做 Perceptron Hypothesis 。PLA算法就是要根据训练数据找出最优的$w_i$和$threshold$。
- 具体到上面的实例,$x={x_1, x_2}$只有两维特征,代入$h(x)$中进行简化:
- 接着把所有的训练样本x1和x2绘制到二维平面上(根据方程$w_1x_1+w_2x_2-threshold=0$来绘制):
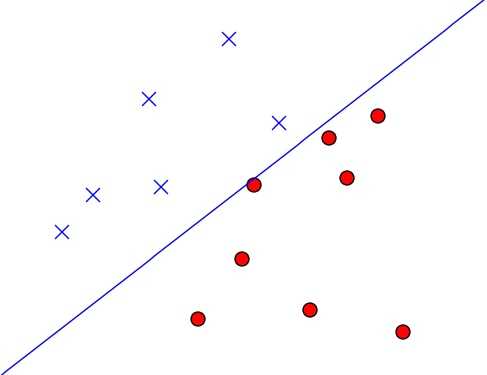
- 可以看到是一条直线,左边的点$w_1x_1+w_2x_2-threshold<0$,右边的点$w_1x_1+w_2x_2-threshold>0$,可以推出:PLA假设集合中任意一个确定的$h(x)$,都可视作一条直线将平面分隔成了两个区域。线的左边有$h(x)=-1$,右边有$h(x)=1$。
- 至此学习算法希望选中的模型就是上述的直线$g$,正好将训练数据划分为两个区域;可以知道该预测函数就是一个线性分类器。事实上你会发现这样的直线存在很多条,那究竟如何选择一条最优的直线呢?也即确定最优的$W_i$和$threshold$的解。
- 将所有的$-threshlod$记作$w_0$,并给所有的$x$增加一个维度$x_0$,所有的$x_0$设为1;这样就可以将$threshlod$收到$w$中,PLA找到最优的那条线即等价于找到最优的参数$w$。
-
接下里就是具体的算法实现了: 1. 随便找一条线,即任意找一个n维向量$w_0$,赋初值另$w = w_0$ 2. 如果这条线正好把训练数据正确切分,Lucky!!训练结束!!此时$w$代表的$h(x)$就是我们学得的模型$g$ 3. 如果有任意一个样本没有被切分正确,即存在任意$(x’, y’)$,使得$sign(w^T x’) != y’$,此时我们对w代表的线做一点点修正,另$W_t+1 = w_t + y’x$ 4. 跳转到Step 2
- 该算法的核心就是步骤三中的修正原理:
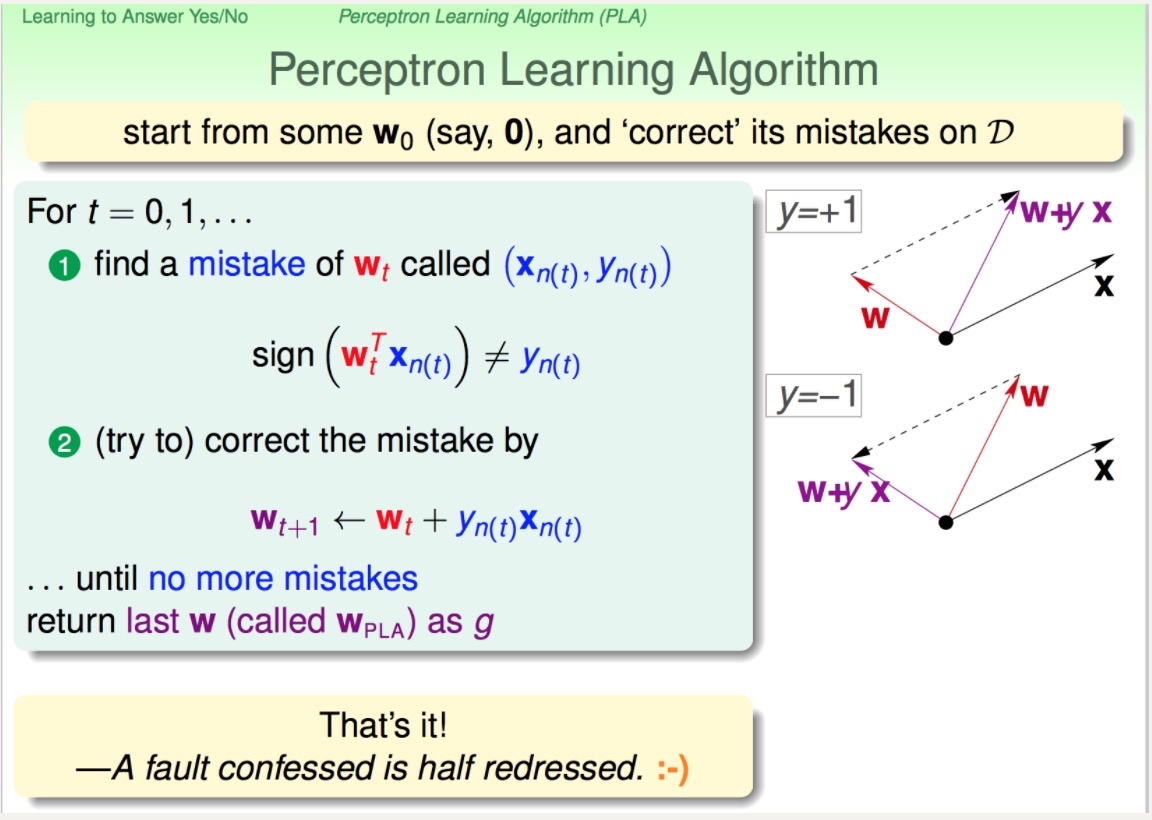
- 修正原理解释:以右上角的图形向量表示为例,$w$和$x$向量的夹角大于90度, 也就是说这两个向量的内积是负的,$sign(wx)$的结果就是-1,而我们需要的$y$则是+1,所以我们需要去修正这个内积的结果,使得它的符号是正的。只需要修正向量$w$的取值,保证新的$w$向量和$x$向量的夹角是小于90度的,这样我们对这个点的划分就是正确的。如上图所示我们将$w$更新为$w+yx$,这样根据四边形法则求内积结果符号就是正的。那这个更新公式是怎么来的呢?$y = +1$,$w+xy=w+x$ 刚好将向量的夹角变小了,当然根据实际情况还可以添加系数$t$,令$w=w+t* xy$。注:两个向量的夹角大于90度,则向量内积就是负的,小于90度,向量内积是正的,可以直观的从图形上看出来。
sign = lambda x:1 if x > 0 else -1 if x < 0 else -1 sign(2) = 1
#lambda表达式含义:lambda x:(1 if x > 0) else (-1 if x < 0) else -1 #上述语句可以转换成: def g(x): if(x > 0) return 1 else if(x < 0) return -1 else return -1
- 具体的代码参见:
- 这里有个问题就是:PLA算法一定可以停下来吗?答案是否定的。PLA算法不一定会停下来,如果训练数据本身就不存在一条线可以将其正确切分,那么学习的过程将进入死循环。所以:训练数据是线性可分的,是PLA能够学习的必要条件
- 过拟合(神经网络)参考
- 产生的情形:模型参数太多,而训练样本太少
- 现象(表现):模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低
- 解决方式:一般采用模型集成的方式,但是训练费时
- 过拟合和费时也便成了训练深度神经网络遇到的两大缺点
- 更优的解决方式:Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果
- 通过阻止特征检测器的共同作用来提高神经网络的性能
- 概念:dropout可以作为训练深度神经网络的一种trick方式。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
- 简言之,在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征
- 理论过程:随机删除一半隐藏神经元,在修改后的网络中经过前向和反向传播之后更新权重和偏置;恢复删除的神经元,再随机删除一半的隐藏神经元,继续上述过程,更新权重和偏置。
- 具体实现:关键是如何让一部分隐藏神经元停止工作,也即删除掉?代码层面是如何实现的。采用dropout的网络计算公式中关键的一环就是采用伯努利概率让某些神经元以概率p停止工作,也即让它们的激活函数值以概率p变为0。比如某一层的网络神经元的个数为1000个,其激活函数输出值为$y_1、y_2、y_3、……、y_{1000}$,我们dropout比率选择0.4,那么这一层神经元经过dropout后,1000个神经元中会有大约400个的值被置为0。
- 【注意】屏蔽上述神经元将其激活函数值变为0之后,还需要对$y_1、y_2、y_3、……、y_{1000}$进行缩放,即乘以$1/(1-p)$。
- Dropout解决过拟合的原理:
- 取平均的作用:先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout删除掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
- 减少神经元之间复杂的共适应关系:因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
- Dropout类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
- keras中Dropout源码
- 修改版(dropout函数可以单独运行):
#coding:utf-8
import numpy as np
#dropout函数的实现
def dropout(x, level):
if level < 0. or level >= 1: #level是概率值,必须在0~1之间
raise ValueError('Dropout level must be in interval [0, 1[.')
retain_prob = 1. - level
#我们通过binomial函数,生成与x一样的维数向量。binomial函数就像抛硬币一样,我们可以把每个神经元当做抛硬币一样
#硬币正面的概率为p,n表示每个神经元试验的次数
#因为我们每个神经元只需要抛一次就可以了所以n=1,size参数是我们有多少个硬币。
random_tensor = np.random.binomial(n=1, p=retain_prob, size=x.shape)#即将生成一个0、1分布的向量,0表示这个神经元被屏蔽,不工作了,也就是dropout了
print(random_tensor)
x *= random_tensor
print(x)
x /= retain_prob
return x
#对dropout的测试,大家可以跑一下上面的函数,了解一个输入x向量,经过dropout的结果
x=np.asarray([1,2,3,4,5,6,7,8,9,10],dtype=np.float32)
dropout(x,0.4)
- 函数中$x$是本层网络的激活值,Level就是dropout就是每个神经元要被丢弃的概率。【注】Keras中Dropout的实现,是屏蔽掉某些神经元,使其激活值为0以后,对激活值向量x1……x1000进行放大,也就是乘以1/(1-p)。
思考
- Droopout为啥要进行缩放?因为我们训练的时候会随机的丢弃一些神经元,但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元,这会带来结果不稳定的问题,也就是给定一个测试数据,有时候输出a有时候输出b,结果不稳定,这是实际系统不能接受的,用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个p,这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是x,那么在训练的时候它有p的概率参与训练,(1-p)的概率丢弃,那么它输出的期望是px+(1-p)0=px。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望
- 总结:当前Dropout被大量利用于全连接网络,而且一般认为设置为0.5或者0.3,而在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积网络隐藏层中使用较少。总体而言,Dropout是一个超参,需要根据具体的网络、具体的应用领域进行尝试。
最优化问题
- 参数和超参数:模型$f(x, \theta)$中的${\theta}$就是模型的参数,而类似聚类算法中的类别个数、梯度下降法的步长、正则项的系数、神经网络的层数、支持向量机中的核函数等,这些很难通过优化算法自动学习的一般是超参数。
- (批量)梯度下降、随机梯度下降、小批量随机梯度下降